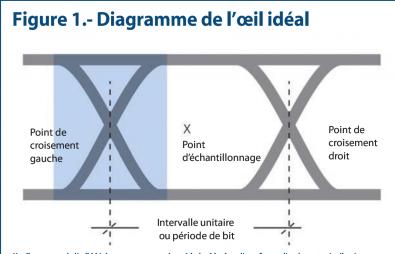
Un diagramme de l'œil idéal superpose toutes les périodes binaires d'une forme d'onde capturée. Il présente ainsi des transitions très lisses et symétriques aux points de croisement gauche et droit. Un grand « œil », largement ouvert au centre, montre l'emplacement idéal (« x ») pour échantillonner chaque bit.

P ourquoi les ordinateurs sont-ils numériques ? Une partie de la réponse se trouve dans le fait que la conversion en nombres binaires des signaux représentant le monde autour de nous et variant constamment permet de préserver plus facilement les informations contenues dans ces signaux tout au long des traitements ultérieurs, plutôt que de travailler directement sur un signal analogique. Néanmoins, même si la plupart du temps les « 1 » et les « 0 » d'un train de bits numériques se distinguent aisément les uns des autres, ces bits sont encore représentés sous forme de signaux électriques traversant un monde analogique sujet au bruit.

Si un bruit électrique suffisamment élevé affecte un signal numérique, il peut provoquer une « gigue » de la forme d'onde binaire ou un retard temporel. Des problèmes surviennent alors si le niveau auquel un signal passe de « 0 » à « 1 », ou de « 1 » à « 0 », est décalé au point que sa valeur soit mal interprétée à l'étape d'échantillonnage. Lorsque cela se produit, donc, le circuit de réception peut mal interpréter la valeur binaire de la forme d'onde, introduisant une erreur de transmission. Il existe différents types de gigue, et la compréhension des caractéristiques de chacun peut aider les ingénieurs à identifier les causes de la gigue et à agir pour les atténuer.

On identifie trois principales causes de gigue : les phénomènes propres au système, ceux dépendant des données et les phénomènes de bruit aléatoire. Les phénomènes propres au système sont des effets sur un signal qui résultent directement de sa condition de système numérique au sein d'un environnement analogique. On peut citer, comme exemples de telles sources, la diaphonie à partir de signaux rayonnés ou conduits, les effets de la dispersion et les désadaptations d'impédance.

En ce qui concerne les phénomènes dépendant des données, ils sont liés à la séquence des données transférées et comprennent l'interférence entre les symboles, la distorsion du rapport cyclique et la périodicité de la séquence de bits pseudo-aléatoire. Enfin, les sources de gigue liées aux phénomènes de bruit aléatoire incluent le bruit thermique, le bruit thermique blanc (exprimé par la relation kTB, où k est la constante de Boltzmann, T la température et B la bande passante du bruit) – il est fonction du flux d'électrons dans les conducteurs et qui augmente avec la bande passante, la température et la résistance –, le bruit « shot » qui correspond à celui des électrons et des trous au sein des semi-conducteurs – l'amplitude de ce bruit est fonction du courant de polarisation et de la bande passante de mesure – et le bruit « rose » (bruit fréquentiel lié à l'inverse de la fréquence).

Des sources de gigue bornées et non bornées

Les sources de gigue sont souvent classées comme « bornées » ou « non bornées ». Les sources de gigue bornées, ou déterministes, atteignent des valeurs d'écart de phase maximales et minimales dans un intervalle de temps identifiable. Ce type de gigues relève de phénomènes systématiques et dépendant des données, tels que présentés dans les deux premiers groupes mentionnés auparavant. Les sources de gigue non bornées, ou aléatoires, n'ont aucune limite concernant la valeur du décalage de phase, quel que soit l'intervalle de temps, et l'amplitude de gigue de ces sources peut (en théorie) être infinie.

La gigue totale sur un signal, spécifiée comme une fonction d'erreur de phase, est ainsi la somme des composantes de gigue déterministes et aléatoires affectant ledit signal. La composante de gigue déterministe est calculée en ajoutant les valeurs maximales d'avance de phase (ou de temps) et de retard de phase (ou de temps) produits par les sources de gigue déterministes. La composante de gigue aléatoire, elle, regroupe toutes les sources de bruit aléatoires affectant le signal. On suppose que la gigue aléatoire suit une distribution gaussienne et est définie par la moyenne et l'écart-type de cette distribution gaussienne.

Avec sa forme irrégulière, un diagramme de l'œil plus réaliste fournit une mine d'informations sur le signal, sans avoir à recourir à des mesures plus complexes. Le fait que la partie basse de la forme d'onde présente, par exemple, une plus petite variation en amplitude que la partie haute semble indiquer que le signal transporte plus de « 0 » que de « 1 ».

Lorsque l'on s'intéresse à la gigue d'un signal, on parle immanquablement de diagramme de l'œil. Un diagramme de l'œil idéal ( voir figure 1 ) superpose toutes les périodes binaires d'une forme d'onde capturée. Ce diagramme de l'œil présente des transitions très lisses et symétriques aux points de croisement gauche et droit. Un grand « œil », largement ouvert au centre, montre l'emplacement idéal (« x ») pour échantillonner chaque bit. À ce point d'échantillonnage, la forme d'onde doit être bien établie à sa valeur haute, ou basse, et sa lecture est donc très peu susceptible de provoquer une erreur de bit. La figure 2 montre un diagramme de l'œil plus réaliste, cette forme fournissant beaucoup d'informations sur le signal sans avoir à recourir à des mesures plus complexes.

Cet histogramme montre une gigue sur la période d'un signal d'horloge. La bosse gauche de l'histogramme semble avoir une forme gaussienne normale. Par contre, les deux pics du côté droit suggèrent que le signal comprend des harmoniques du deuxième et quatrième ordre qui causent la gigue.

Par exemple, le fait que la partie basse de la forme d'onde présente une plus petite variation en amplitude que la partie haute semble indiquer que le signal transporte plus de « 0 » que de « 1 ». Il y a également quatre trajectoires différentes dans la partie du bas, d'où la présence possible d'au moins quatre « 0 » à la suite. Au sommet de la forme d'onde, il y a tout au plus deux trajectoires, donc la forme d'onde peut contenir au maximum deux « 1 » de suite. La forme d'onde ayant deux fronts différents en montée et en descente, cela signifie que la forme d'onde est soumise à une gigue déterministe. Enfin, les fronts montants sont plus éta-lés que les fronts descendants, et certains des points de croisement se situent au-dessous du niveau de seuil. Cela indique que les rapports cycliques sont distordus : les « 0 » semblent durer plus longtemps que les « 1 ».

Une deuxième façon de visualiser la gigue est la courbe en baignoire. Dans ce cas de figure est représenté le taux d'erreur binaire (BER) d'un signal par rapport à son point d'échantillonnage. L'axe horizontal correspond au temps nécessaire pour transmettre un symbole unique, et l'axe vertical, le taux d'erreur binaire sur une échelle logarithmique.

D'autres façons de visualiser une gigue

Il existe toutefois d'autres façons de visualiser la gigue, et, si plusieurs d'entre elles sont appliquées au même signal, cela peut aider à identifier les sources de gigue et, ainsi, indiquer les moyens de la réduire. La première de ces façons est l'histogramme : les valeurs relevées pour un paramètre choisi (souvent le temps ou l'amplitude) sont portées sur l'axe x et leur fréquence d'occurrence, sur l'axe y. Pour l'analyse de gigue, les histogrammes sont utiles pour représenter des paramètres de la forme d'onde tels que le temps de montée, le temps de descente, la période ou le rapport cyclique, ou encore pour mettre en évidence des distributions multimodales qui peuvent alors être corrélées avec des conditions de circuit comme les séquences de bits transmis.

Des histogrammes peuvent également être utilisés pour établir des ensembles de données essentielles pour la mise en œuvre des routines de séparation de gigue, routines requises par diverses normes de bus numériques. Une attention particulière doit être apportée au paramétrage de la mesure de gigue sur horloge, au choix du (ou des) front(s) à mesurer et du seuil de mesure. L'histogramme de la figure 3 montre une gigue sur la période d'un signal d'horloge. La bosse gauche de l'histogramme semble avoir une forme gaussienne normale. Par contre, les deux pics du côté droit suggèrent que le signal comprend des harmoniques du deuxième et quatrième ordre qui causent la gigue. Une nouvelle analyse de la gigue de l'horloge séparant les fronts montants des fronts descendants permettra d'identifier quel front présente le plus de gigue.

Une deuxième façon de visualiser la gigue est la courbe en baignoire : celle représentée à la figure 4 montre le taux d'erreur binaire ( Bit Error Rate ou BER) d'un signal par rapport à son point d'échantillonnage, en affichant sur l'axe horizontal le temps nécessaire pour transmettre un symbole unique. Le BER est représenté sur une échelle logarithmique, pour montrer la relation entre celui-ci et le point d'échantillonnage. Lorsque le point d'échantillonnage se situe aux points de transition, ou à proximité, le BER est égal à 0,5, ce qui signifie que la probabilité que la transmission d'un bit réussisse, ou échoue, est la même. Dans ces régions, la courbe est assez plate et la gigue déterministe domine. Lorsque le point d'échantillonnage s'éloigne du point de transition, le BER décroît rapidement. Ces régions sont plutôt soumises au processus de gigue aléatoire, dont les effets additionnés affectent le BER. La courbe en bai-gnoire montre que le meilleur moment pour échantillonner le signal, soit celui avec le BER le plus bas, se trouve à mi-chemin entre le début et la fin du temps de transmission du symbole.

Une autre façon d'analyser la gigue consiste à considérer la distribution en fréquence des spectres de bruit de phase ou de gigue (ici, un spectre de gigue intrinsèque d'une boucle à verrouillage de phase). Des sources de gigue déterministes peuvent ainsi être détectées, car leurs raies de fréquence apparaissent sur le tracé.

Enfin, une autre façon d'analyser la gigue consiste à considérer la distribution en fréquence des spectres de bruit de phase ou de gigue. Des sources de gigue déterministes peuvent ainsi être détectées, car leurs raies de fréquence apparaissent sur le tracé. Ce type de visualisation peut également révéler un bruit de phase ou des décalages de gigue, selon la fréquence, à partir d'une porteuse ou d'une horloge. Les mesures de bruit de phase fournissent des informations utiles pour la conception de boucles à verrouillage de phase (PLL) ou d'oscillateurs à cristal, et elles aident à identifier une gigue déterministe induite par des signaux parasites. De telles mesures sont également utiles pour optimiser les circuits de récupération d'horloge et pour détecter toute source interne de parasite et de bruit.

N'oublions pas une bonne FFT

La figure 5 montre, par exemple, le spectre de gigue intrinsèque d'une boucle à verrouillage de phase (PLL). Le

bruit se situe à un offset de 2 kHz, et des sources de gigue déterministes apparaissent également à des fréquences de 60 Hz à environ 800 Hz, ce qui indique qu'elles sont dues à des signaux parasites générés par les lignes d'alimentation. Des pics sont également visibles à 2 et 7 MHz et sont plus susceptibles d'être des signaux parasites dérivés de l'horloge de référence, provoquant ainsi une gigue déterministe. Une autre méthode pour apercevoir de la gigue dans le domaine fréquentiel consiste à réaliser une transformée de Fourier rapide (FFT) des erreurs d'intervalle de temps ( Time Interval Error ou TIE), qui sont définies comme la différence de phase entre le signal mesuré et l'horloge de référence. La FFT donne, certes, un aperçu beaucoup moins précis et ne permet pas de visualiser le bruit de phase de faible intensité, mais elle est utile pour révéler rapidement et facilement des phénomènes de niveau plus élevé.

Résoudre les problèmes de gigue est une partie essentielle du développement de produits. Pour analyser l'impact global des gigues déterministes et non bornées, une combinaison de différentes techniques de mesure, telles que des diagrammes de l'œil, des histogrammes, des courbes en baignoire et l'analyse dans le domaine fréquentiel, peut fournir des informations utiles. Une fois que les ingénieurs ont identifié et compris les sources de gigue dans leurs conceptions, ils disposent de beaucoup plus de moyens pour réduire cette gigue, voire l'éliminer, améliorant ainsi la performance de transmission de leurs conceptions.

Andrea Dodini, European Marketing Manager chez Keysight Technologies Article adapté par Cédric Lardière